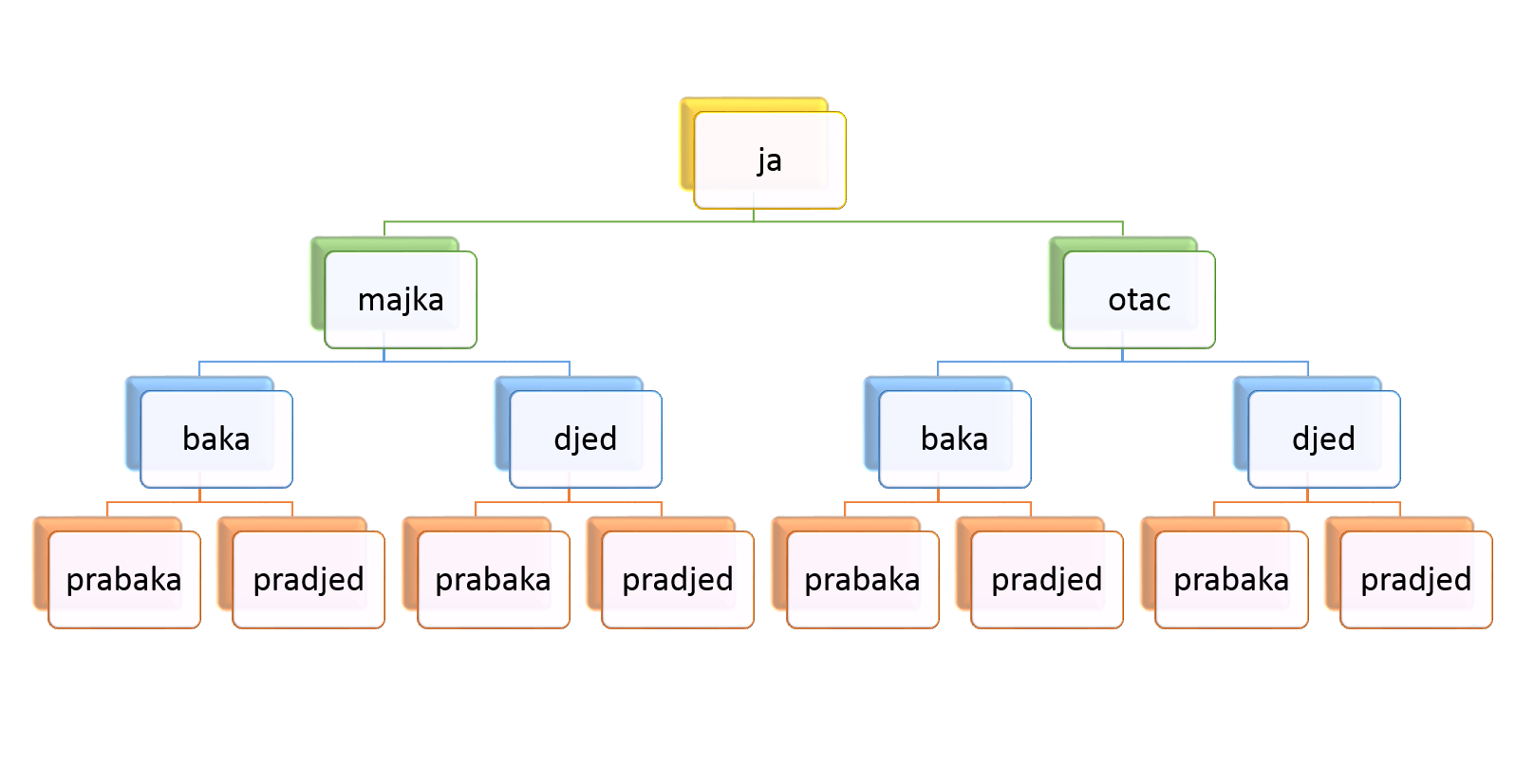
Marija je razgovarala sa svojom mamom o njezinim roditeljima, Marijinoj baki i djedu. Pitala je mamu sjeća li se svoje bake i djeda pa onda i prabake i pradjeda. Marija je odlučila istražiti svoje korijene: bake i djedove, prabake i pradjedove. Na papiru je počela slagati prikaz. Pazila je da su u jednom redu osobe iz iste generacije. Za ženske je osobe stavljala zeleni kružić, a za muške osobe plavi kružić. Pokraj crteža zapisivala je broj osoba u generaciji. Primijetila je da broj osoba jako brzo raste, toliko da više ne može nastaviti s prikazom. Isto tako, uočila je pravilnost u tome kako nastaju brojevi.
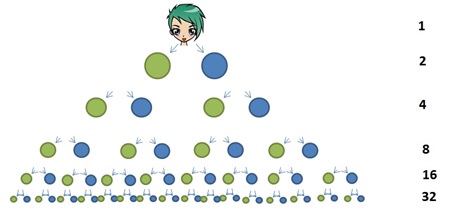
Odredite pravilnost koja povezuje napisane brojeve?
Brojevi koje je dobila, mogu biti napisani kao umnožak broja sa samim sobom.
Odredite koji će biti sljedeći broj u prikazu.
Sljedeći je broj u prikazu jer je
Primjer 1.
Brojeve možemo skraćeno zapisati i čitati:
čitajmo "dva na drugu"
čitajmo "dva na treću"
čitajmo "dva na četvrtu"
čitajmo "dva na petu"
čitajmo "dva na šestu".
U izrazu broj množimo sa samim sobom puta.
Zapis
nazivamo potencija s bazom
i eksponentom
Baza je potencije broj koji množimo sa samim sobom. Eksponent je broj koji broji koliko je puta baza pomnožena sa samom sobom.
Uparite potenciju s prirodnom bazom i prirodnim eksponentom s njezinim značenjem kao umnoškom jednakih faktora i iznosom.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Proučimo kako se mijenja vrijednost potencije kada je:
Pri nepromijenjenom eksponentu, što je baza veća, veća je i vrijednost potencije.
Ako je onda je za
Pri nepromijenjenoj bazi, što je eksponent veći, veća je i vrijednost potencije.
Ako je
onda je
za
Usporedite potencije s jednakim eksponentima.
Poredajte, od najmanje do najveće, potencije bez izračunavanja njihove vrijednosti.
Pomoć:
Od dvije potencije istog prirodnog eksponenta manja je ona koja ima manju prirodnu bazu.
Usporedite potencije s jednakim bazama.
Poredajte od najmanje do najveće potencije bez izračunavanja njihove vrijednosti.
Pomoć:
Od dvije potencije jednakih prirodnih baza manja je ona koja ima manji prirodni eksponent.
U sljedećoj aktivnosti uvježbajte značenje zapisa potencijom s prirodnim eksponentom.
U sljedećoj aktivnosti ispravno uparite potenciju i njezinu vrijednost.
Izračunajte naizmjenično eksponent, bazu i vrijednost potencije tako da jednakost bude valjana.
Primjer 2.
Prikažimo broj kao potenciju.
Potencija mora imati bazu i eksponent.
Potencija s eksponentom jedan ima vrijednost jednaku bazi te potencije.
Potencija broja uvijek je jednaka
Primjena potencije za rješavanje problema
Na stolu je deset kutija. U svakoj je kutiji deset manjih kutijica. U svakoj se manjoj kutijici nalazi
lipa. Koliko je kuna u tih
kutija?

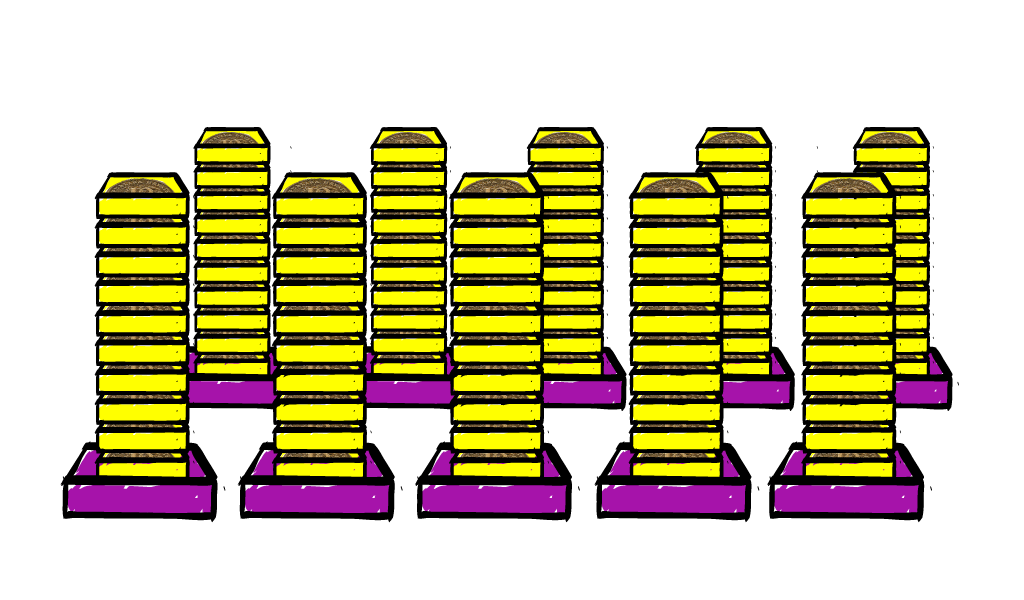
U deset je kutija na stolu
lipa, što iznosi
kuna.
Marija je u školi učila o potencijama s prirodnom bazom i prirodnim eksponentom. Htjela se uvjeriti koliko brzo raste iznos novca koji će štedjeti prema potenciji s bazom Na ormarić je stavila šest kutijica.
Prvog je dana u prvu kutiju stavila
Drugog je dana u drugu kutiju stavila trostruko više novca.
Zatim je svaki dan, sljedeća četiri dana, u jednu od kutija stavila trostruko više novca nego prethodnog dana.
Koliko je novca Marija stavila šesti dan u šestu kutiju?
Šesti dan u šestoj kutiji bilo je
kune.
Koliko bi kuna bilo deseti dan u desetoj kutijici?
Uočili smo pravilnost u kojoj je iznos kuna jednak vrijednosti potencije s bazom a u eksponentu je broj za jedan manji od broja dana pa je tako šesti dan iznos bio kune.
Deseti bi dan štednje u desetoj kutijici bilo kuna.
Zamislite štedjeti na sljedeći način:
Prvi dan odvojite pet kuna, drugi dan puta više i svaki sljedeći dan pet puta više nego prethodni.
Koliko biste novca uštedjeli samo peti dan?
Samo biste peti dan uštedjeli
kuna.
U sljedećem će videu biti pokazano kako koristiti džepno računalo za izračunavanje potencije s prirodnom bazom i eksponentom.
Bit će pokazana tri načina:
Koristeći džepno računalo, potenciju možemo računati na tri različita načina.
Koristeći džepno računalo, provjerite vrijednost potencije.
U sljedećem će videu biti pokazano kako prirodni broj prikazati potencijom.
Primjer 3.
Potenciranje je računska operacija trećeg stupnja i ima prednost nad množenjem i dijeljenjem te zbrajanjem i oduzimanjem.
Dovucite zadani rastav na proste faktore pripadnom prirodnom broju.
Uparivanje odgovora.
|
|
|
|
|
|
|
|
|
|
|
|
Primjer 4.
Proučimo najprije potencije s negativnom bazom i neparnim eksponentom.
Potencija s negativnom bazom i neparnim eksponentom ima negativnu vrijednost.
Ako je neparan:
Primjer 5.
Proučimo sada potencije s negativnom bazom i parnim eksponentom.
Potencija s negativnom bazom i parnim eksponentom ima pozitivnu vrijednost.
Ako je
paran:
U sljedećem nizu zadataka izračunajte potenciju s negativnom bazom.
Izračunajmo obujam kocke kojoj je duljina brida
Obujam kocke računamo tako da pomnožimo duljinu, širinu i visinu kocke.
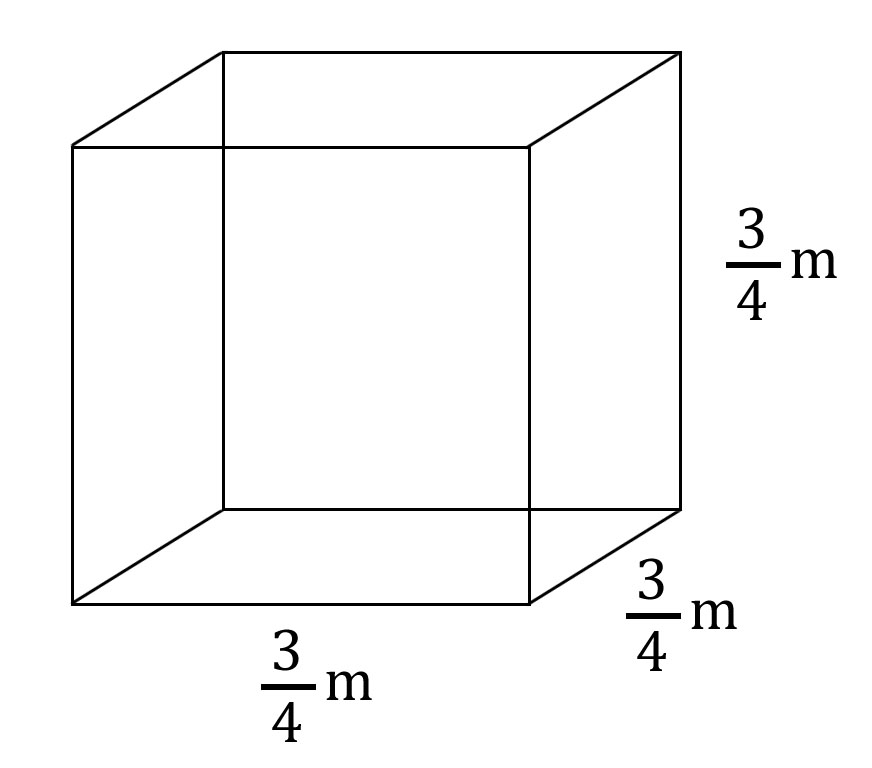
Pomnožimo dimenzije zapisane u obliku razlomka. Umnožak je razlomaka razlomak koji u brojniku ima umnožak brojnika, a u nazivniku umnožak nazivnika.
U brojniku se pojavila potencija broja a u nazivniku broja
Umnožak broja sa samim sobom n puta n-ta je potencija tog broja.
Obujam kocke brida duljine iznosi
Potencija razlomka prirodnim brojem jednaka je razlomku koji u brojniku ima brojnik potenciran prirodnim brojem a u nazivniku nazivnik potenciran prirodnim brojem .
uz uvjete
U sljedećim zadatcima izračunajte i odaberite točnu vrijednost zadane potencije.
Odredite točnost zadanih jednakosti.
Primjer 6.
Poredajmo, od najveće prema najmanjoj, vrijednosti zadanih potencija. Uočimo da imaju jednake pozitivne baze manje od jednog cijelog:
Primijetimo, što je eksponent veći, to je manja vrijednost potencije.
Ako je baza potencije veća od a manja od vrijednost se potencije smanjuje što je eksponent veći.
Bez izračunavanja vrijednosti potencija, poredajte ih od najveće do najmanje.
Poredajte:
Pomoć:
Za potencije baze između i vrijedi da je to manja što je eksponent veći.
Razlomci između nula i jedan imaju brojnik manji od nazivnika.
Bez izračunavanja vrijednosti potencija, poredajte ih od najveće do najmanje.
Poredajte:
Pomoć:
Za potencije baze između i vrijedi da je to manja što je eksponent veći.
Zadana je kocka duljine brida
Koliki je obujam te kocke u metrima kubičnim?
Obujam kocke brida duljine metara iznosi .
U zadatku koji slijedi, okušajte se u računanju s potencijama.
Poštujte redoslijed računskih radnji: prvo potenciranje, a onda množenje ili dijeljenje.
Možete se poslužiti i džepnim računalom.
Ako točno riješite zadatak, čeka vas iznenađenje!
U animaciji ćete naučiti kako utvrditi je li neki prirodni broj potencija prirodnog broja korištenjem rastava broja na faktore.
Primjer 7.
Koristeći rastav na proste faktore, odgovorite na pitanja u zadatku.
Je li
potencija broja
Je li
potencija broja
Je li
potencija broja
Je li
potencija broja
Dva su brata sakupljala kovanice.
Jedan je imao pet kutija. U svakoj je kutiji bilo pet manjih kutijica, a u svakoj toj kutijici kovanica od kuna.
Drugi je imao tri kutije, u svakoj tri manje kutije, u svakoj još tri manje kutije, u svakoj još tri još manje kutije s po tri kune.
Koji je brat sakupio više novca?
Na prvoj je slici Sierpinskijev sag.
Proces njegova nastajanja prikazan je na drugoj slici.
Koliko je zelenih kvadrata u petom koraku?
Primjećujemo da je ukupan broj kvadrata u svakom sljedećem koraku puta veći od njihova broja u prethodnom koraku.
Koliko je zelenih kvadrata u petom koraku?
Primjer 8.
Preračunajmo mjerne jedinice za duljinu. Rezultat prikažimo u obliku potencija.
Primjer 9.
Preračunajmo mjerne jedinice za površinu. Rezultat prikažimo u obliku potencija.
Primjer 10.
Preračunajmo mjerne jedinice za obujam. Rezultat prikažimo u obliku potencija.
Preračunajte i zapišite koristeći potenciju s bazom
Dovucite odgovarajuće izraze na njihove jednakosti.
Uparite:
|
|
|
|
|
|
|
|
|
|
|
|
Odredite je li zadana jednakost točna.
Koliko litara vode stane u plastičnu posudu oblika kocke čija je duljina brida
Prvi način:
Izračunajmo obujam te kocke u kubičnim metrima.
Obujam kocke jednak je umnošku duljina njezinih bridova.
Kako su svi bridovi kocke duljine obujam kocke računamo
Preračunajmo kubične metre u kubične decimetre.
U tu posudu stane litara vode.
Drugi način:
Preračunajmo duljinu stranice u decimetre jer je
Izračunajmo obujam u kubičnim decimetrima.
U tu posudu stane litara vode.
Istražite povijest svoje obitelji i napravite stablo nasljeđivanja kako je to učinila Marija.
Pokušajte u razgovoru sa svojim roditeljima, bakama i djedovima saznati što više imena svojih direktnih predaka i upišite ih.
Prebrojite koliko se svojih predaka sjećate u pojedinoj generaciji.
U kojoj se generaciji gubi svaki trag imenima?
Koliko je tvojih direktnih predaka u petoj, šestoj... generaciji?