Matematika 8 - 3.3 Množenje i dijeljenje korijena

Na početku...

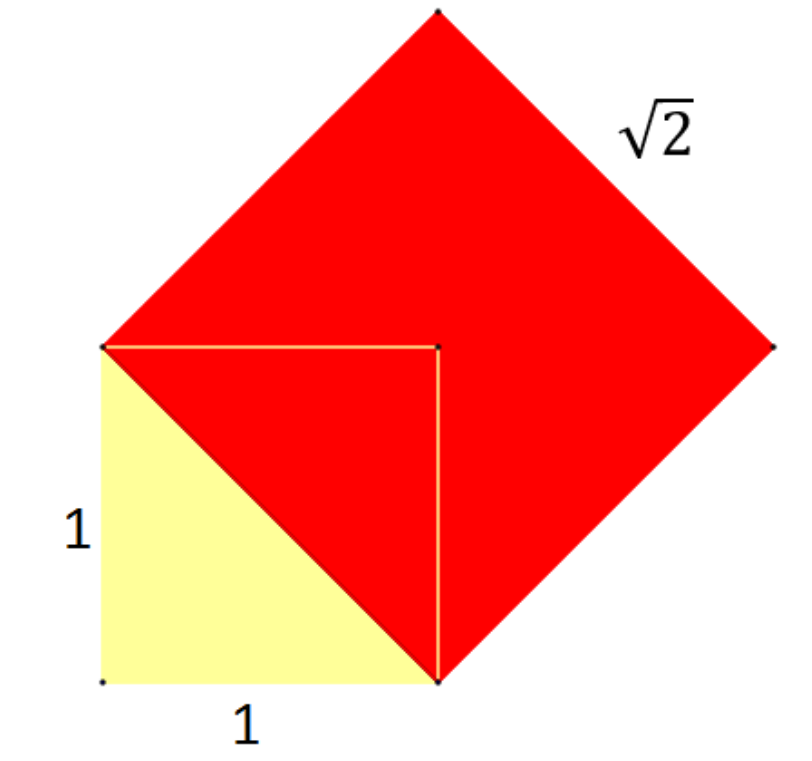
Slika kvadrata s još jednim kvadratom nad njegovom dijagonalom.

Lorena je nacrtala kvadrat sa stranicom duljine $1 cm$ i jednu njegovu dijagonalu. Nad tom dijagonalom nacrtala je novi kvadrat. U kojem su odnosu površina novoga i početnoga kvadrata? Rješenje možete provjeriti s pomoću animacije.

Površina početnog kvadrata iznosi $1\cdot1=1{cm}^{2} .$

Površina novog kvadrata iznosi $\sqrt{2} \cdot \sqrt{2} = {\sqrt{2}}^{2} .$

S obzirom na to da su kvadriranje i korjenovanje suprotne računske radnje, vrijedi:

${\sqrt{a}}^{2} = a, a \geq 0 .$

Zato je ${\sqrt{2}}^{2} = 2 .$

Dakle, površine novoga i početnoga kvadrata odnose se u omjeru $2 : 1 .$

Zadatak 1.

Izračunajte.

$13^{2}$
$(- 13)^{2}$
$- 13^{2}$

Prema definiciji kvadriranja imamo:

$13^{2} = 13 \cdot 13 = 169$
$(- 13)^{2} = - 13 \cdot (- 13) = 169$
$- 13^{2} = - 13 \cdot 13 = - 169.$

Zanimljivost

Prisjetimo se, broj $a$ i $- a$ suprotni su brojevi.

Kvadrati su suprotnih brojeva jednaki.

To zapisujemo $a^{2} = (- a)^{2} = {|a|}^{2} .$

Broj $- a^{2}$ suprotan je broju $a^{2}$ pa su zato i njihovi predznaci različiti.

Možemo opaziti da se u izrazu $- a^{2}$ prvo izvodi računska radnja kvadriranja, a zatim se određuje broj suprotan broju $a^{2} .$

Primjer 1.

Odredimo:

${\sqrt{3}}^{2}$

$\sqrt{3^{2}}$

$\sqrt{(- 7)^{2}}$

$\sqrt{- 7^{2}} .$

${\sqrt{3}}^{2} = \sqrt{3} \cdot \sqrt{3} = 3$
$\sqrt{3^{2}} = \sqrt{3 \cdot 3} = \sqrt{9} = 3$
$\sqrt{(- 7)^{2}} = \sqrt{49} = 7$
$\sqrt{- 7^{2}} = \sqrt{- 49}$

Kvadrati su svih racionalnih brojeva veći ili jednaki nuli, tj. ne postoji racionalni broj koji kvadriranjem poprima negativnu vrijednost. Zato u skupu racionalnih brojeva ne postoji drugi korijen negativnog broja. Zbog toga zadatak nema rješenje.

Kvadrat korijena nenegativnoga racionalnog broja jednak je samom tom broju.

${\sqrt{a}}^{2} = a$ za $a \geq 0 .$

Korijen kvadrata nekog broja i korijen kvadrata njemu suprotnog broja jednaki su apsolutnoj vrijednosti tog broja.

$\sqrt{a^{2}} = \sqrt{(- a)^{2}} = |a|$ za $a \in Q .$

Prisjetimo se, $\sqrt{- 16}$ nema rješenje u skupu racionalnih brojeva.

Razvrstajete zadane brojeve.

{\sqrt{25}}^{2}

- 5 \sqrt{- 5}

\sqrt{- 100}

\sqrt{7^{2}}

\sqrt{(- 3)^{2}}

\sqrt{256}

\sqrt{9}

\sqrt{- 121}

Imaju rješenje u skupu racionalnih brojeva

Nemaju rješenje u skupu racionalnih brojeva

null

Množenje korijena

Primjer 2.

Koristeći se u tablici zadanim podatcima, odredi vrijednost nepoznatih podataka računajući u bilježnici (na papir).

$a$ $b$ $a \cdot b$
$\sqrt{a}$
$\sqrt{b}$ $\sqrt{a \cdot b}$ $\sqrt{a} \cdot \sqrt{b}$

$1$
$4$

$4$ $9$

$0$ $36$

$2.25$ $0.25$

$\frac{4}{25}$ $\frac{9}{16}$

Što zamjećujemo?

$a$	$b$	$a \cdot b$	$\sqrt{a}$	$\sqrt{b}$	$\sqrt{a \cdot b}$	$\sqrt{a} \cdot \sqrt{b}$
$1$	$4$	$4$	$1$	$2$	$2$	$2$
$4$	$9$	$36$	$2$	$3$	$6$	$6$
$0$	$36$	$0$	$0$	$6$	$0$	$0$
$2.25$	$0.25$	$0.5625$	$1.5$	$0.5$	$0.75$	$0.75$
$\frac{4}{25}$	$\frac{9}{16}$	$\frac{9}{100}$	$\frac{2}{5}$	$\frac{3}{4}$	$\frac{3}{10}$	$\frac{3}{10}$

Zamjećujemo da su korijen umnoška i umnožak korijena nenegativnih racionalnih brojeva jednaki (to su brojevi u posljednja dva stupca).

Zaključujemo da je $\sqrt{a} \cdot \sqrt{b} = \sqrt{a \cdot b}$ za $a \geq 0$ i $b \geq 0 .$

Vrijedi i obratno, $\sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b}$ za $a \geq 0$ i $b \geq 0 .$

Umnožak korijena dvaju nenegativnih racionalnih brojeva jednak je korijenu njihova umnoška.

Korijen umnoška dvaju nenegativnih racionalnih brojeva jednak je umnošku njihovih korijena.

Primjer 3.

Izračunajte koristeći se svojstvom umnoška korijena.

$\sqrt{2} \cdot \sqrt{8}$

$\sqrt{8} \cdot \sqrt{18}$

$\sqrt{2} \cdot \sqrt{5}$

$3 \sqrt{2} \cdot 2 \sqrt{7}$

$\sqrt{2} \cdot \sqrt{8} = \sqrt{16} = 4$
$\sqrt{8} \cdot \sqrt{18} = \sqrt{144} = 12$
$\sqrt{2} \cdot \sqrt{5} = \sqrt{10}$
$3 \sqrt{2} \cdot 2 \sqrt{7} = 6 \sqrt{14}$

Primjer 4.

Izračunajte koristeći se svojstvom korijena umnoška.

$\sqrt{1 440 000}$

$\sqrt{2.56 \cdot 10^{6}}$

$\sqrt{4 y^{2} x^{2}}$

$\sqrt{1 000^{4}}$

$\sqrt{1 440 000} = \sqrt{144} \cdot \sqrt{10 000} = 12 \cdot 100 = 1 200$
$\sqrt{2.56 \cdot 10^{6}} = \sqrt{2.56} \cdot \sqrt{10^{6}} = 1.6 \cdot 10^{3}$
$\sqrt{4 y^{2} x^{2}} = \sqrt{4} \cdot \sqrt{y^{2}} \cdot \sqrt{x^{2}} = 2 y x$
$\sqrt{1 000^{4}} = \sqrt{(10^{3})^{4}} = \sqrt{10^{12}} = 10^{6}$

Zadatak 2.

Kutak za znatiželjne

Je li za sve racionalne brojeve korijen umnoška jednak umnošku korijena? Ako jest, objasnite. Ako nije, napišite primjer u bilježnicu.

$\sqrt{(- 9) \cdot (- 1)} = \sqrt{9} = 3,$ ali $\sqrt{- 9} \cdot \sqrt{- 1} \neq 3 .$

Korijen umnoška jednak je umnošku korijena i obratno samo za nenegativne racionalne brojeve.

Prisjetimo se, u skupu racionalnih brojeva ne postoji drugi korijen negativnog broja, zato drugi zadatak nema rješenja.

Dijeljenje korijena

Primjer 5.

Koristeći se u tablici zadanim podatcima, odredi vrijednost nepoznatih podataka računajući u bilježnici (na papir).

$a$ $b$ $a : b$ $\sqrt{a}$ $\sqrt{b}$ $\sqrt{a : b}$ $\sqrt{a} : \sqrt{b}$

$0$ $49$

$1$ $4$

$25$ $64$

$0.09$ $0.0001$

Što zamjećujemo?

$a$	$b$	$a : b$	$\sqrt{a}$	$\sqrt{b}$	$\sqrt{a : b}$	$\sqrt{a} : \sqrt{b}$
$0$	$49$	$0$	$0$	$7$	$0$	$0$
$1$	$4$	$\frac{1}{4}$	$1$	$2$	$\frac{1}{2}$	$\frac{1}{2}$
$25$	$64$	$\frac{25}{64}$	$5$	$8$	$\frac{5}{8}$	$\frac{5}{8}$
$0.09$	$0.0001$	$900$	$0.3$	$0.01$	$30$	$30$

Zamjećujemo da su korijen količnika i količnik korijena nenegativnih racionalnih brojeva jednaki (to su brojevi u posljednja dva stupca tablice).

Zaključujemo da je

$\sqrt{a} : \sqrt{b} = \sqrt{a : b}$ za $a \geq 0$ i $b > 0 .$

Vrijedi i obratno, $\sqrt{a : b} = \sqrt{a} : \sqrt{b}$ za $a \geq 0$ i $b > 0 .$

Količnik korijena dvaju nenegativnih racionalnih brojeva jednak je korijenu njihova količnika.

Korijen količnika dvaju nenegativnih racionalnih brojeva jednak je količniku njihovih korijena.

Primjer 6.

Koristeći se svojstvom količnika korijena, izračunajte.

$\sqrt{75} : \sqrt{3}$

$\sqrt{\frac{225}{361}}$

$\sqrt{225 : 49}$

$\sqrt{\frac{1}{8}} : \sqrt{\frac{9}{2}}$

$\sqrt{75} : \sqrt{3} = \sqrt{25} = 5$
$\sqrt{\frac{225}{361}} = \frac{\sqrt{225}}{\sqrt{361}} = \frac{15}{19}$
$\sqrt{225 : 49} = \sqrt{225} : \sqrt{49} = 15 : 7 = \frac{15}{7}$
$\sqrt{\frac{1}{8}} : \sqrt{\frac{9}{2}} = \sqrt{\frac{1}{8} \cdot \frac{2}{9}} = \sqrt{\frac{1}{4} \cdot \frac{1}{9}} = \sqrt{\frac{1}{36}} = \frac{1}{6}$

Zadatak 3.

Izračunajte.

$\sqrt{0.08} : \sqrt{0.02}$
$\sqrt{\frac{16}{25}} : \sqrt{2 \frac{7}{9}}$
$\sqrt{\frac{- 121}{- 225}}$
$\sqrt{49 a^{2} : b^{2}}$

$\sqrt{0.08} : \sqrt{0.02} = \sqrt{0.08 : 0.02} = \sqrt{4} = 2$
$\sqrt{\frac{16}{25}} : \sqrt{2 \frac{7}{9}} = \sqrt{\frac{16}{25}} : \sqrt{\frac{25}{9}} = \frac{4}{5} : \frac{5}{3} = \frac{4}{5} \cdot \frac{3}{5} = \frac{12}{25}$
$\sqrt{\frac{- 121}{- 225}} = \sqrt{\frac{121}{225}} = \frac{\sqrt{121}}{\sqrt{225}} = \frac{11}{15}$
$\sqrt{49 a^{2} : b^{2}} = \sqrt{49 a^{2}} : \sqrt{b^{2}} = 7 a : b = \frac{7 a}{b}$

Množenje i dijeljenje korijena

Primjer 7.

Pojednostavnimo izraze.

$(\sqrt{3} + 1) (\sqrt{5} - 2 \sqrt{2})$

$(3 \sqrt{3} + 2 \sqrt{5})^{2}$

$(4 - 5 \sqrt{6}) (4 + 5 \sqrt{6})$

$(\sqrt{7} - \sqrt{3})^{2}$

$(\sqrt{3} + 1) (\sqrt{5} - 2 \sqrt{2}) = \sqrt{15} - 2 \sqrt{6} + \sqrt{5} - 2 \sqrt{2}$
$(3 \sqrt{3} + 2 \sqrt{5})^{2} = 27 + 12 \sqrt{15} + 20 = 47 + 12 \sqrt{15}$
$(4 - 5 \sqrt{6}) (4 + 5 \sqrt{6}) = 16 - 150 = - 134$
$(\sqrt{7} - \sqrt{3})^{2} = 7 - 2 \sqrt{7} \cdot \sqrt{3} + 3 = 10 - 2 \sqrt{21}$

Zadatak 4.

Povežite zadatke s njima odgovarajućim rješenjima.

$2 \sqrt{3} - 3 \sqrt{5} - (\sqrt{3} + 2 \sqrt{5})$	$57 + 12 \sqrt{15}$
$(2 \sqrt{3} - 3 \sqrt{5})^{2}$	$\sqrt{3} - 5 \sqrt{5}$
$(2 \sqrt{3} + 3 \sqrt{5}) (2 \sqrt{3} - 3 \sqrt{5})$	$57 - 12 \sqrt{15}$
$(2 \sqrt{3} + 3 \sqrt{5})^{2}$	$- 33$

null

Primjer 8.

Izračunajte.

$\sqrt{2} \cdot \sqrt{3} \cdot \sqrt{6} \cdot {\sqrt{2}}^{2}$

$\frac{\sqrt{(- 7)^{2}}}{\sqrt{44} : \sqrt{11}}$

$\sqrt{\frac{24}{147}} \cdot \sqrt{\frac{1}{6}} : \sqrt{\frac{4}{27}}$

$(\sqrt{5} + 3 \sqrt{3}) (2 \sqrt{3} - 7 \sqrt{2})$

$\sqrt{2} \cdot \sqrt{3} \cdot \sqrt{6} \cdot {\sqrt{2}}^{2} = \sqrt{36} \cdot 2 = 6 \cdot 2 = 12$
$\frac{\sqrt{(- 7)^{2}}}{\sqrt{44} : \sqrt{11}} = \frac{7}{\sqrt{4}} = \frac{7}{2}$
$\sqrt{\frac{24}{147}} \cdot \sqrt{\frac{1}{6}} : \sqrt{\frac{4}{27}} = \sqrt{\frac{24}{147} \cdot \frac{1}{6} : \frac{4}{27}} = \sqrt{\frac{24}{147} \cdot \frac{1}{6} \cdot \frac{27}{4}} = \sqrt{\frac{9}{49}} = \frac{3}{7}$
$(\sqrt{5} + 3 \sqrt{3}) (2 \sqrt{3} - 7 \sqrt{5}) = 2 \sqrt{15} - 35 + 18 - 21 \sqrt{15} = - 17 - 19 \sqrt{5}$

Zadatak 5.

Izračunajte.

$\sqrt{5} \cdot \sqrt{15} \cdot \sqrt{3}$
$\frac{\sqrt{33} \cdot \sqrt{28}}{\sqrt{77}}$
$\sqrt{1 \frac{2}{5}} : \sqrt{\frac{10}{121}} \cdot \sqrt{\frac{9}{14}}$
$\sqrt{(- \sqrt{3})^{2} \cdot \sqrt{(- 3)^{2}}}$

$\sqrt{5} \cdot \sqrt{15} \cdot \sqrt{3} = \sqrt{225} = 15$
$\frac{\sqrt{33} \cdot \sqrt{28}}{\sqrt{77}} = \sqrt{\frac{33 \cdot 28}{77}} = \sqrt{\frac{3 \cdot 28}{7}} = \sqrt{\frac{3 \cdot 4}{1}} = \sqrt{12}$
$\sqrt{1 \frac{2}{5}} : \sqrt{12 \frac{1}{10}} \cdot \sqrt{\frac{9}{14}} = \sqrt{\frac{7}{5} : \frac{121}{10} \cdot \frac{9}{14}} = \sqrt{\frac{7}{5} \cdot \frac{10}{121} \cdot \frac{9}{14}} = \sqrt{\frac{9}{121}} = \frac{3}{11}$
$\sqrt{(- \sqrt{3})^{2} \cdot \sqrt{(- 3)^{2}}} = \sqrt{3 \cdot 3} = \sqrt{9} = 3$

Poredajte izraze od onog čija je vrijednost najmanja do onog čija je vrijednost najveća.

$(3 \sqrt{2} - \sqrt{5}) (3 \sqrt{2} + \sqrt{5})$
$\sqrt{2} \cdot \sqrt{18}$
$15 \sqrt{\frac{89}{100} - 0.25}$
$\frac{2}{3} \sqrt{8} \cdot \sqrt{2} + \sqrt{49} : \sqrt{9} + \sqrt{20} \cdot \sqrt{5}$

null

Pogledajte kako se rješavaju neki složeniji zadatci.

Rješavanje složenijih zadataka

Kutak za znatiželjne

Kinetička je energija energija koju tijelo ima dok se giba, a ovisi o masi i brzini tijela.

Kinetička energija računa se prema formuli $E_{k} = \frac{1}{2} m v^{2},$ gdje je masa izražena u kilogramima, a brzina u metrima u sekundi.

Marta se bavi skokovima u vodu. Netom prije doticaja s vodom, Martina kinetička energija iznosi $3 500 J .$

Ako je Martina masa $40 kg,$ kolika je njezina brzina izražena u metrima u sekundi?

$3 500 = \frac{1}{2} \cdot 40 \cdot v^{2}$

$3 500 = 20 \cdot v^{2}$

$175 = v^{2}$

$v = \sqrt{175}$

$v \approx 13 \frac{m}{s}$

Martina brzina približno iznosi $13 m/s .$

Napomena: Kvadratna jednadžba ima dva rješenja, pozitivno i negativno, no u ovom slučaju negativna brzina nema smisla.

$\sqrt{3} (\sqrt{3} - \sqrt{2})$	$- 1$
$(\sqrt{2} + \sqrt{3})^{2}$	$5 + 2 \sqrt{6}$
$(\sqrt{2} - \sqrt{3}) (\sqrt{2} + \sqrt{3})$	$5 - 2 \sqrt{6}$
$(\sqrt{2} - \sqrt{3})^{2}$	$3 - \sqrt{6}$

3.3 Množenje i dijeljenje korijena

Na početku...

Zadatak 1.

Zanimljivost

Imaju rješenje u skupu racionalnih brojeva

Nemaju rješenje u skupu racionalnih brojeva

Množenje korijena

Zadatak 2.

Kutak za znatiželjne

Dijeljenje korijena

Zadatak 3.

Množenje i dijeljenje korijena

Zadatak 4.

Zadatak 5.

Kutak za znatiželjne

...i na kraju

Kutak za znatiželjne

MOJE ZNANJE

Uspješno ste usvojili sve odgojno-obrazovne ishode:

Potrudite se još malo kako biste bolje usvojili sljedeće odgojno-obrazovne ishode:

Trebali biste ponovno proći sljedeće jedinice:

3.4 Djelomično korjenovanje